【Day 17】比我還單純的語言？電腦的世界只有 0 和 1！

比我還單純的語言？電腦的世界只有 0 和 1

基本上只要上電腦課，我幾乎都會用「強制關閉」這招來擺脫老師的控制。但有一次，不知道為什麼，突然心血來潮（對，就是這麼突然），想要好好聽聽老師到底在講什麼。

「在電腦的世界裡，你們所看到的一切都是由 0 和 1 組成的。」老師在白板上寫著。

「蛤？什麼？電腦的世界只有 0 和 1？那顏色怎麼來的？」我心裡冒出疑問。

「是不是很好奇顏色怎麼產生的？其實顏色也是由 0 和 1 組成的。」老師彷彿讀心術般地接著說。

「大家應該還記得 RGB 三元素吧？R 代表 Red（紅）、G 代表 Green（綠）、B 代表 Blue（藍），這三個顏色組合起來就能產生各種色彩。」老師一邊說著一邊在白板上畫了三個圓圈，分別標上 R、G、B。

「就連畫面上的 A、B、C 這些字母，也是由 0 和 1 組成的。要靠一個東西，叫做 ASCII。」老師寫下大大的「ASCII」。

「WOW！原來電腦沒辦法直接看懂 A、B、C 啊！」我心裡覺得挺酷炫的。
……不過沒多久我就棄聽課，照慣例跑去打遊戲了。

「ㄟ，XXX，你們魔獸爭霸打完沒？」我邊用「強制關閉」技巧解除老師的控制，邊轉頭問同學。

「快打完了，你下一場要打嗎？」同學一邊專注操控角色，一邊回我。

「好啊，要不要用 GGC 跟路人對打？」我問。

Note
GGC 是一個社群遊戲平台，由於魔獸爭霸僅能在區域網路（LAN）對戰，所以玩家會透過 GGC 來模擬區域網路，進而與其他玩家進行對戰。

「好啊！」同學回答。

相信你各位應該都知道沒聽課的下場是什麼了，電腦課的考試和課後作業，我根本一題都寫不出來。

二進位 Binary

什麼是二進位呢？二進位又稱 Binary，它是一套數字系統，僅用兩個符號來做代表，也就是數字的 0 和 1。

「二進位只有電腦有嗎？」你可能會有這樣的疑問。

不對，只要跟電子電路有關的東西都是使用二進位，那為什麼會採用二進位呢？難道不能用其他進位嗎？像是八進位、十進位、十六進位等等的？

其實原因有兩個：

• 二進位的電路設計相對簡單，因為它只需要兩種狀態：開（1）和關（0），這使得電路更容易被設計與實現。
• 二進位對於電子訊號的容錯率相對較高。

這邊有些名詞可能對於讀者稍微比較陌生，所以我在這邊也同時解釋一下「容錯率」與「電子訊號」的意思。

首先容錯率（Fault Tolerance）是指系統在遇到錯誤或故障時的忍受範圍，也就是系統能夠在某些部分失效的情況下仍然能夠繼續運作，你也可以理解為「明明出錯了，但系統還是能夠繼續運作」的意思。

那麼電子訊號呢？

電子訊號（Electrical Signal）是在指電路中傳遞的電壓變化，這些變化可以用於表示數字，例如：0V ~ 0.8V 代表 0，而 2V ~ 5V 代表 1，而 0.8V ~ 2V 則是代表不確定的狀態，又稱為「雜訊」。

在電子訊號裡，有一個很容易被誤解的觀念：「電子訊號 ≠ 資料」。
電子訊號指的是電壓的變化，而資料則是這些變化所承載的意義。換句話說，電子訊號只是資料的「載體」，但它本身不等於資料。

舉個例子，假設我們要傳遞數字 5，它的二進位表示是 101。轉換成電子訊號後，可能會變成「5V、0V、5V」，這組電壓變化就代表數字 5，接著電腦會再把它解讀回 101。

那麼這邊要來說明一個關鍵問題：

「5 是怎麼變成 101 的呢？」

這邊就會牽扯到二進位的表示方式了。

首先，要介紹二進位之前，我們先認識一下我們平常最常使用的「十進位」。

十進位（Decimal）就是我們日常使用的數字系統，使用 0 到 9 這十個符號來表示數字。當從 0 數到 9 之後，下一個數字「10」的產生方式是：個位歸零，前一位進一，這就是「進位」的概念。

那麼二進位呢？它只使用 0 和 1 兩個符號。當數到「2」時，因為已經超出範圍，個位數會歸零，前一位進一，所以就從「1」變成「10」。

接下來我們來試一道小小的練習題，示範如何把十進位轉換成二進位。

「請試著將十進位的數字 13 轉換成二進位。」

別擔心，接下來我會手把手帶你一步步完成。

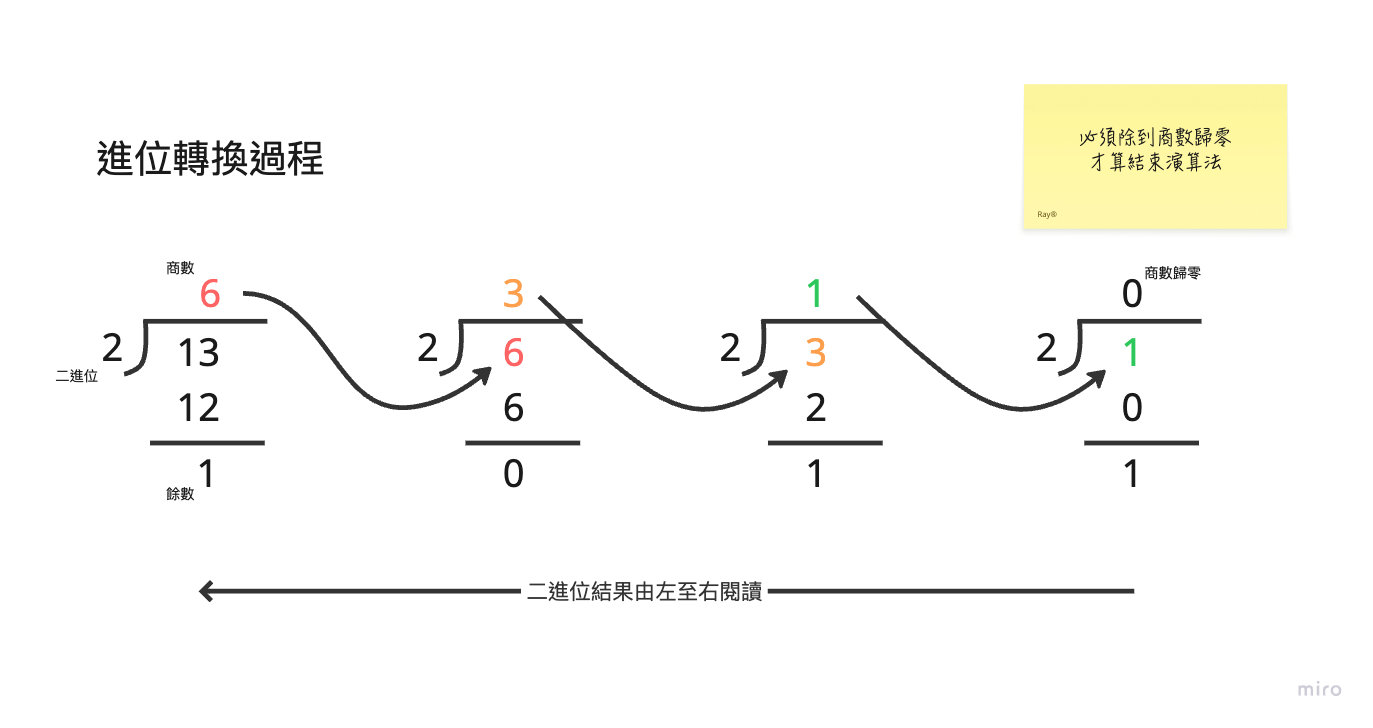
做法是「不斷除以 2，並記下餘數」，直到商數為 0 為止：

• 13 ÷ 2 = 6，餘數 1
• 6 ÷ 2 = 3，餘數 0
• 3 ÷ 2 = 1，餘數 1
• 1 ÷ 2 = 0，餘數 1

Note
所謂的「商數」指的是除法的結果，而「餘數」則是除法後剩下的部分。

接著我們將餘數從下往上排列（最後一個 → 最前一個）：

→ 1101

所以十進位的數字 13，換成二進位就是：1101

看到這邊應該會有人冒出一個疑問：

「13 ÷ 2 不是應該是 6.5 嗎？為什麼會是 6 呢？」

這是因為在數學裡，像 6.5 這種帶小數的結果屬於「實數除法」，但在做二進位轉換時，我們用的是「整數除法」，也就是只取整數部分，把小數點後的部分直接捨去，至於被捨去的小數部分，就會變成我們所說的「餘數」。

那餘數為什麼是 1 呢？ 以最直接的方式來看：

• 13 ÷ 2 = 6 …… 餘 1
• 因為2 × 6 = 12，剛好小於 13。
• 13 − 12 = 1，這就是餘數。

以表格來表示的話，會是這樣：

實數除法	整數除法
13 ÷ 2 = 6.5	13 ÷ 2 = 6 餘數 1
6 ÷ 2 = 3	6 ÷ 2 = 3 餘數 0
3 ÷ 2 = 1.5	3 ÷ 2 = 1 餘數 1
1 ÷ 2 = 0.5	1 ÷ 2 = 0 餘數 1

那有辦法驗證我們的答案嗎？當然可以，將二進位的 1101 轉換回十進位：

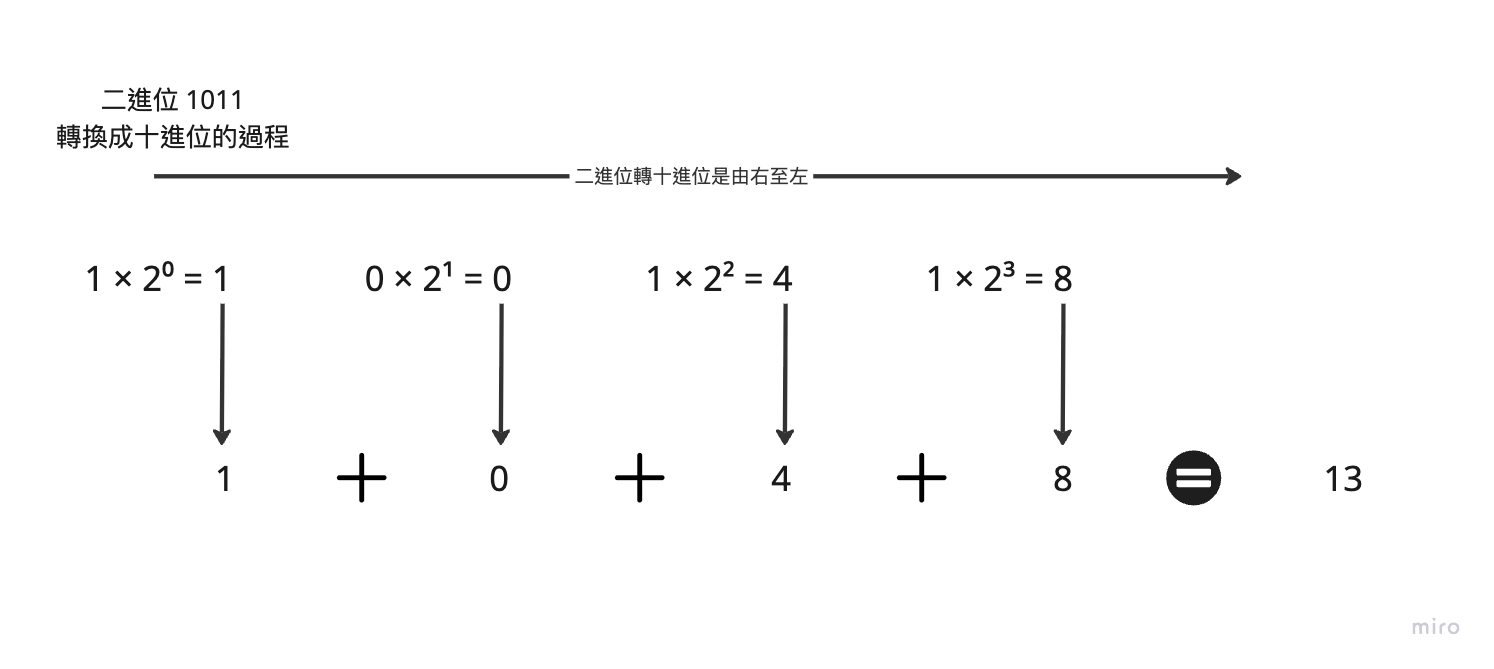
1101（二進位）從右到左分別代表：

• 1 × 2⁰ = 1
• 0 × 2¹ = 0
• 1 × 2² = 4
• 1 × 2³ = 8

將這些數字加總起來：1 + 0 + 4 + 8 = 13

這樣就證明了我們的轉換是正確的。

那麼這時候可能會冒出一個疑問：電腦到底是怎麼儲存這些二進位數字？又是如何把它們轉換成我們能理解的文字呢？
這些內容，我會在下一篇文章中再跟大家分享！

同步更新

本文將同步更新至以下網站：

• 是 Ray 不是 Array
• Code Review 我的青春：從『嗶』聲開啟我的軟體工程師之路（佛心分享-IT 人自學之術）
• Threads - 時常會聊軟實力
• Facebook - 搞怪迷因分享
• Instagram - 搞怪迷因分享 + 軟實力
• Portaly - 入口主頁